Plan Representation: #1 Lesson Learned from Building an Optimizer

Table of Contents

• Introduction
• A Simple IR: One Big Enum
• A Simple Transformation: Join Commutativity
• A Heuristics Optimizer Framework
• A Cost-Based Optimizer Framework
• Apply the Rules Again: Transformations in the Memo Table
• A New Plan Representation

Introduction

Now, we are going to write a SQL query optimizer. The first thing we will need to decide is how to store the plan in memory — the representation of the plan.

Say that we have a query:

CREATE TABLE t1(x INT, y INT, z INT);
CREATE TABLE t2(y INT);
SELECT * FROM t1, t2 WHERE t1.y = t2.y AND t1.z = 3;

We will likely get a query plan like this: ^{^1}

Filter #2 (t1.z) = 3
  Join #1 (t1.y) = #3 (t2.y)
    Scan t1
    Scan t2

How do we store such query plans in Rust? I mean, if we need to write a function like this:

fn get_plan() -> RelNode {
  return ...
}

How do we define RelNode, and what do we put at ... to construct the plan? This is a big question that we want to answer.

A Simple IR: One Big Enum

[code for this section]

One thing people can quickly come up with is to have a structure representing each of the plan nodes, where each structure has multiple named fields to store the children and properties of the plan node. For example,

pub struct Scan {
    pub table: TableId,
}

pub struct Join {
    pub left: Arc<RelNode>,
    pub right: Arc<RelNode>,
    pub cond: Arc<RelNode>,
}

pub struct Filter {
    pub child: Arc<RelNode>,
    pub predicate: Arc<RelNode>,
}

Then, we can have a big enum representing all entities in the query language,

pub enum RelNode {
    Scan(Scan),
    Join(Join),
    Filter(Filter),
    Eq(EqPred),
    ColumnRef(ColumnRefPred),
    Const(ConstPred),
}

With some helper functions to convert the types and wrap them into Arc automatically:

pub fn join(
    left: impl Into<Arc<RelNode>>,
    right: impl Into<Arc<RelNode>>,
    cond: impl Into<Arc<RelNode>>,
) -> RelNode {
    RelNode::Join(Join {
        left: left.into(),
        right: right.into(),
        cond: cond.into(),
    })
}

We can then construct the plan:

pub fn plan() -> RelNode {
    filter(
        join(
            scan(TableId(0)),
            scan(TableId(1)),
            eq_pred(column_ref_pred(1), column_ref_pred(3)),
        ),
        eq_pred(column_ref_pred(2), const_pred(3)),
    )
}

Everything sounds so good, right (for now)?

A Simple Transformation: Join Commutativity

[code for this section]

We stored the plan in memory, and the optimizer kicks in and does its work. The job of a query optimizer is to rewrite the plan into another plan that is (potentially) more efficient to execute. An example rewrite is to apply the commutativity of join operators. “A inner join B” should yield the same result as “B inner join A”. Let’s do this transformation. ^{^2}

pub fn join_commute(node: Arc<RelNode>) -> Option<Arc<RelNode>> {
    if let RelNode::Join(ref a) = &*node {
        return Some(join(a.right.clone(), a.left.clone(), a.cond.clone()).into());
    }
    None
}

So, if the join_commute transformation sees a join plan node, it will return an equivalent rewritten plan (in terms of the execution result) that swaps the join order. If it does not see a join plan node, it returns None, which means we cannot rewrite that plan node.

Such transformations can be defined in a more generic form called rules. A rule takes a plan and rewrites it into another plan that produces the same result. The user provides the optimizer with a set of rules, and the optimizer decides when and where to fire these rules and finds out if the rewritten plan is better than the original one.

So now we have a plan representation, some plan nodes, and a rule. We can start building a query optimizer!

A Heuristics Optimizer Framework

[code for this section]

We have defined a rule. Rules only apply to a single plan node, but a plan is a tree — we can’t apply a rule only to the root; we need to apply the rule recursively to the plan tree. Take the original query as an example. The join plan node is the child of the filter plan node. We must start from the root of the plan, go down recursively, and apply that rule.

A heuristics optimizer applies rules on plan nodes using a specified order. Users usually provide rules known to improve the quality of a query plan in ordinary cases to the heuristics optimizer, who will apply the rules whenever possible. For example, in 99% of the cases, turning a nested loop join with an equal join condition into a hash join would be a good choice, and pushing filters down will reduce the amount of computation performed. On the contrary, a cost-based optimizer will use the cost model to determine whether it’s good or not to apply a rule that allows users to define transformations that are not always good.

Generally, there are two applying orders for each rule: top-down and bottom-up. It’s easier to explain them by code:

fn apply_rule_bottom_up(
    node: Arc<RelNode>,
    rule: &impl Fn(Arc<RelNode>) -> Option<Arc<RelNode>>,
) -> Arc<RelNode> {
    // Get optimized children
    let mut children = Vec::new();
    for child in node.children() {
        let child = apply_rule_bottom_up(child, rule);
        children.push(child);
    }
    let rel = create_new_plan_node(node, children);
    // Apply the rule after all children are processed
    rule(rel.clone()).unwrap_or(rel)
}

fn apply_rule_top_down(
    node: Arc<RelNode>,
    rule: &impl Fn(Arc<RelNode>) -> Option<Arc<RelNode>>,
) -> Arc<RelNode> {
    // Apply the rule before all children are processed
    let node = rule(node.clone()).unwrap_or(node);
    // Get optimized children
    let mut children = Vec::new();
    for child in node.children() {
        let child = apply_rule_top_down(child, rule);
        children.push(child);
    }
    create_new_plan_node(node, children)
}

The order of application does not matter for the join commutativity rule — we will always get the same result if join commutativity is the only rule in the system. It is not a good example as a rule for a heuristics optimizer because we cannot know which join order is better without having a cost model. So, let’s look at another example to illustrate the rule application order: the filter pushdown rules. We can push the filter past the projection node if we find a pair of filter-projection plan nodes.

As in the figure above, applying the filter-projection rule in a top-down order will push the filter down to the scan node, while applying it in a bottom-up order will only push it one level down.

In a heuristics optimizer, despite the order of applying a rule on the plan nodes, we also need to determine which rule to apply first (the order of invocation) and how many times we need to apply a rule (we can apply a rule multiple times). We will cover them in later blog posts.

Back to the topic of plan representation. Can we implement a generic function apply_rule_bottom_up that takes a rule and a plan node and produces an optimized plan? Now, here’s the challenge. We need to get all children of the plan nodes and clone the plan nodes with a new set of children. We need a trait on all the plan nodes or a function on the RelNode enum to retrieve/modify such information.

impl Join {
    pub fn children(&self) -> Vec<Arc<RelNode>> {
        vec![self.left.clone(), self.right.clone(), self.cond.clone()]
    }

    pub fn clone_with_children(&self, children: Vec<Arc<RelNode>>) -> Self {
        Self {
            left: children[0].clone(),
            right: children[1].clone(),
            cond: children[2].clone(),
        }
    }
}


impl RelNode {
    pub fn children(&self) -> Vec<Arc<RelNode>> {
        match self {
            RelNode::Join(join) => join.children(),
            RelNode::Filter(filter) => filter.children(),
            // ...
        }
    }

    pub fn clone_with_children(&self, children: Vec<Arc<RelNode>>) -> Self {
        match self {
            RelNode::Join(join) => RelNode::Join(join.clone_with_children(children)),
            RelNode::Filter(filter) => RelNode::Filter(filter.clone_with_children(children)),
            // ...
        }
    }
}

Now, we can write the generic function for applying the rule bottom-up:

fn apply_rule_bottom_up(
    node: Arc<RelNode>,
    rule: &impl Fn(Arc<RelNode>) -> Option<Arc<RelNode>>,
) -> Arc<RelNode> {
    // Get optimized children
    let mut children = Vec::new();
    for child in node.children() { // <- defined by the trait
        let child = apply_rule_bottom_up(child, rule);
        children.push(child);
    }
    let rel = Arc::new(node.clone_with_children(children)); // <- defined by the trait
    // Apply the rule after all children are processed
    rule(rel.clone()).unwrap_or(rel)
}

A Cost-Based Optimizer Framework

[code for this section]

With the heuristics optimizer framework, we can rewrite the query plan with rules that we believe will produce a better plan. However, some rules, like the join reordering rule, do not always improve the plan. For example, we can have a set of rules to reorder the joins in the following query,

SELECT * FROM t1, t2, t3 WHERE t1.x = t2.x AND t1.y = t3.y

The initial join order in the plan is (t1 join t2) join t3. All joins have equal conditions. However, if we apply the join reordering set of rules and somehow produce (t2 join t3) join t1, the join between t2 and t3 does not have an equal condition, and we will have to do a nested loop join. The plan is worse than the original plan.

Therefore, to avoid the optimizer generating a worse plan, it must know which one is better. Users can define a cost model to help the optimizer make the decision. We can have a simple cost model that says joins with equal conditions are always better than those without equal conditions. Or we can have a complex statistics-based cost model that uses the histogram and cardinality of the base tables to decide which join order is better.

The simplest way to implement a cost-based optimizer is to enumerate all possible plans by firing all rules until no new plans can be produced by further applying a rule. How many possible plans will we enumerate in this query? ^{^3}

(t1 join t2) join t3
(t2 join t1) join t3
t3 join (t1 join t2)
t3 join (t2 join t1)
(t1 join t3) join t2
(t3 join t1) join t2
t2 join (t1 join t3)
t2 join (t3 join t1)
t1 join (t2 join t3)
t1 join (t3 join t2)
(t2 join t3) join t1
(t3 join t2) join t1

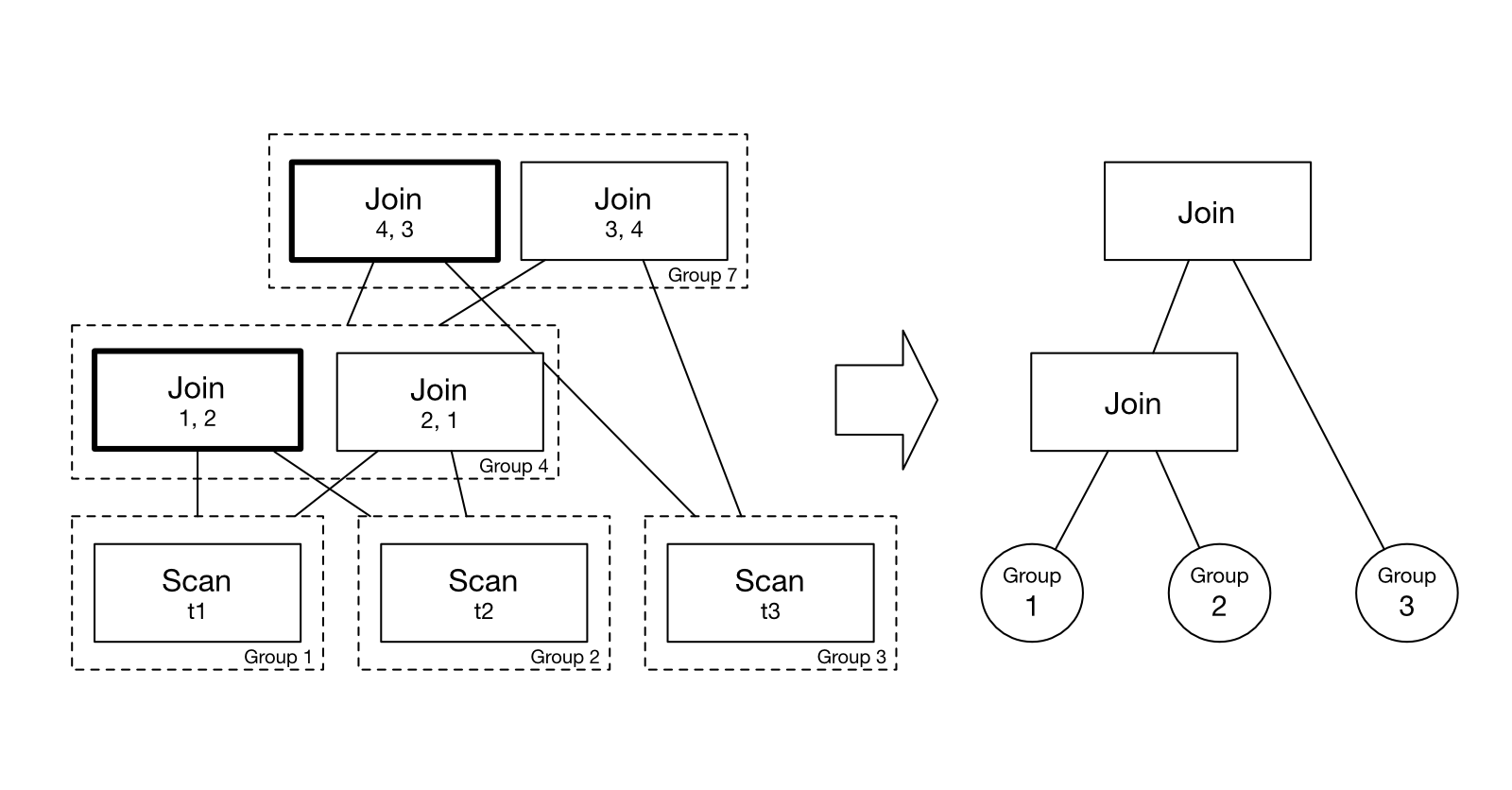
We have a total of 12 possible plans in the plan space. We can fire the cost model on each plan and pick the best one out of them. However, there seem to be a lot of duplicated computations, such as we will need to compute the cost of (t1 join t2) multiple times in two different plans. Plus, (t1 join t2) produces the same result as (t2 join t1), so if we know (t1 join t2) is a better join order than (t2 join t1), we can prune all plans that contains the joins between t1 and t2 but not using the best join order. There is a way to optimize it: we can save the intermediate cost and the winner for an equivalent set of plans for use later.

So here comes the most critical structure in a cost-based optimizer: the memo table. The memo table memorizes the equivalences of the plan subtrees.

• Each equivalence set is a memo table group.
• Each group contains multiple memo table expressions. A memo table expression only contains the plan node with links to the children’s groups. For example, if we want to store (t1 join t2) into the memo table, it will have 3 groups: group 1 containing scan t1, group 2 containing scan t2, and group 3 containing join group1 group2. Note how these plan nodes get flattened into the memo table.
• Each memo table group can have one winner expression. We recursively decide the winner of each group from leaves to roots (i.e., from the scan nodes to the join nodes).

Let’s see how we find the best plan from the memo table. The cost model prefers a smaller table at the left side of the join operator. The estimated number of output rows of join operators is min(left, right). We start from the leaves. As the groups containing scans only have one expression, they are the only winners.

Then, we move to the two-way join nodes, finding the winner in each group. We compute each expression’s cost based on the cost and statistics of the children groups’ winner and select the best expression by comparing the costs.

And finally, for the top-most group 7, we find the winner among the 6 expressions.

As we can see, the best plan is (t1 join t2) join t3, and we can get the best plan by following the winner expressions in the memo table. The memo table helps us avoid duplicated computations by storing each group’s intermediate cost, statistics, and winner.

Going back to the topic of plan representation, how do we store the memo table expressions? It’s clear that we need a new representation of the plans where the children of the plan nodes are GroupId.

#[derive(Copy, Debug, Clone, Hash, Eq, PartialEq)]
pub struct GroupId(usize);

#[derive(Debug, Clone, Hash, Eq, PartialEq)]
pub struct MemoJoin {
    pub left: GroupId,
    pub right: GroupId,
    pub cond: GroupId,
}

#[derive(Debug, Clone, Hash, Eq, PartialEq)]
pub struct MemoFilter {
    pub child: GroupId,
    pub predicate: GroupId,
}

When we get the initial unoptimized plan tree, we need to memorize it in the memo table before applying transformations and deriving the best plan.

pub fn memorize_rel(memo: &mut Memo, rel: Arc<RelNode>) -> GroupId {
    let rel = match &*rel {
        RelNode::Scan(scan) => MemoRelNode::Scan(scan.clone()),
        RelNode::Join(join) => MemoRelNode::Join(MemoJoin {
            left: memorize_rel(memo, join.left.clone()),
            right: memorize_rel(memo, join.right.clone()),
            cond: memorize_rel(memo, join.cond.clone()),
        }),
        RelNode::Filter(filter) => MemoRelNode::Filter(MemoFilter {
            child: memorize_rel(memo, filter.child.clone()),
            predicate: memorize_rel(memo, filter.predicate.clone()),
        }),
        // ... more RelNodes, doesn't seem maintainable
    };
    memo.add_expr(rel)
}

We have covered how to find the winner from the memo table and populate it with the initial plan tree. But how do we apply transformations to the memo table to get multiple expressions in each group?

Apply the Rules Again: Transformations in the Memo Table

[code for this section]

So, we initially have a memo table populated with the initial plan with exactly one expression per group. We can apply transformations to each memo table expression to create more equivalent expressions in the same group.

Join commutativity transformations are straightforward: We can find all nodes like join A B and put join B A back into the same group.

Join associativity transformation seems more complex. We must match on a pattern like join (join A B) C. However, each memo table group only contains one level of the plan tree. Thus, we need first to find all join expressions like join X C, look into group X, and iterate on all join A B from group X. We need then stitch them together to create a thing matching the original matching pattern, and that thing is called a binding.

Note how bindings differ from the original plan tree: In this plan structure, we will have group IDs as leaves. This leads to an unfortunate fact: we need yet another plan representation for rule match bindings.

#[derive(Debug, Clone, Hash, Eq, PartialEq)]
pub struct BindJoin {
    pub left: Arc<BindRelNode>,
    pub right: Arc<BindRelNode>,
    pub cond: Arc<BindRelNode>,
}

#[derive(Debug, Clone, Hash, Eq, PartialEq)]
pub struct BindFilter {
    pub child: Arc<BindRelNode>,
    pub predicate: Arc<BindRelNode>,
}


#[derive(Debug, Clone, Hash, Eq, PartialEq)]
pub enum BindRelNode {
    Scan(BindScan),
    Join(BindJoin),
    // ... Other RelNodes
    Group(GroupId),
}

Once the optimizer produces a binding from the memo table, users can define transformations for that binding to produce an equivalent plan,

 fn join_assoc_memo(node: Arc<BindRelNode>) -> Option<Arc<BindRelNode>> {
    if let BindRelNode::Join(ref a) = &*node {
        if let BindRelNode::Join(b) = &*a.left {
            return Some(Arc::new(BindRelNode::Join(BindJoin {
                left: b.left.clone(),
                right: Arc::new(BindRelNode::Join(BindJoin {
                    left: b.right.clone(),
                    right: a.right.clone(),
                    cond: a.cond.clone(),
                })),
                cond: b.cond.clone(),
            })));
        }
    }
    None
}

To find all bindings that match the join associativity rule, we need a loop to expand the left child of the top match:

pub fn apply_join_assoc_rules_on_node(memo: &mut Memo, group: GroupId, node: MemoRelNode) {
    if let MemoRelNode::Join(node1) = node {
        // Expand the left group of the join
        for expr in memo.get_all_exprs_in_group(node1.left) {
            if let MemoRelNode::Join(node2) = expr {
                let binding = BindJoin {
                    left: Arc::new(BindRelNode::Join(BindJoin {
                        left: Arc::new(BindRelNode::Group(node2.left)),
                        right: Arc::new(BindRelNode::Group(node2.right)),
                        cond: Arc::new(BindRelNode::Group(node2.cond)),
                    })),
                    right: Arc::new(BindRelNode::Group(node1.right)),
                    cond: Arc::new(BindRelNode::Group(node1.cond)),
                };
                let applied = join_assoc_memo(Arc::new(BindRelNode::Join(binding))).unwrap();
                add_binding_to_memo(memo, group, applied);
            }
        }
    }
}

We need yet another function to add bindings back to the memo table:

pub fn add_binding_to_memo(memo: &mut Memo, group: GroupId, node: Arc<BindRelNode>) -> GroupId {
    fn add_binding_to_memo_inner(memo: &mut Memo, node: Arc<BindRelNode>) -> GroupId {
        let node = match &*node {
            BindRelNode::Scan(scan) => MemoRelNode::Scan(scan.clone()),
            BindRelNode::Join(join) => {
                let left = add_binding_to_memo_inner(memo, join.left.clone());
                let right = add_binding_to_memo_inner(memo, join.right.clone());
                let cond = add_binding_to_memo_inner(memo, join.cond.clone());
                MemoRelNode::Join(MemoJoin { left, right, cond })
            }
            BindRelNode::Filter(filter) => {
                let child = add_binding_to_memo_inner(memo, filter.child.clone());
                let predicate = add_binding_to_memo_inner(memo, filter.predicate.clone());
                MemoRelNode::Filter(MemoFilter { child, predicate })
            }
            // ... other RelNodes
            BindRelNode::Group(group) => return *group,
        };
        memo.add_expr(node.clone())
    }
    let new_group = add_binding_to_memo_inner(memo, node);
    if group != new_group {
        memo.merge_group(group, new_group)
    } else {
        group
    }
}

It seems like we are creating chunks of unmaintainable code — every time the user adds a new plan node into the system, they have to modify a lot of places:

1. We need an alternative plan representation for the new plan node’s memo table representation (MemoXXX) and rule-matching binding (BindXXX). Therefore, the user has to define the same plan node in 3 different structures.
2. Users must implement children and clone_with_children for this new plan node so the optimizer can get/modify its children.
3. Users must add such new plan nodes in memorize_rel, add_binding_to_memo, etc., and many other functions that need to convert between different representations of the plan nodes.

From the users’ point of view, they don’t care about and shouldn’t care about how the optimizer works internally (like how the optimizer stores things in the memo table, applies the rules, etc.) In an optimal world, users can tell the optimizer, “Hey, we have these plan nodes, and we have these transformation rules, plus a cost model; please give me the best plan”. The current plan representation and the designs around the plan representation cannot quickly achieve that goal.

Is it possible to design a new plan representation that makes users’ lives easier?

A New Plan Representation

[code for this section]

The plan representation we saw before is widely used in many query optimizers, especially those written in object-oriented programming languages like Java (e.g., Apache Calcite). However, using the exact representation in Rust is much harder because we do not have the same level of polymorphism in Java. If we want to adapt it in Rust, we need to have a separate structure for each representation of the plan node (e.g., RelNode, BindRelNode, and MemoRelNode).

Let’s revisit all the problems we had before again, but from the optimizer framework’s view.

1. The optimizer framework must understand “what’s inside the user’s RelNode enum” to do its job. For example, memorize_rel needs to match the RelNode enum provided by the user in order to transform it into the corresponding memo table expressions and convert it into the corresponding plan bindings when we have a rule match.
2. The core issue is that the optimizer framework needs an easy way to get/manipulate children, and that’s why we need all plan nodes to have children and clone_with_children.
3. The optimizer framework has multiple representations of the same plan node and needs to convert between these representations. For example, memorize_rel converts the initial plan tree into a memo table representation, and apply_join_assoc_rules_on_node converts the memo table representation into a binding.

Can we have a plan representation that is friendly for the optimizer framework to manipulate and pleasant for the user?

Here, I propose to use this new plan representation in the system:

#[derive(Clone)]
pub enum RelNodeType {
    Scan,
    Filter,
    Join,
    Eq,
    ColumnRef,
    Const,
}

pub enum RelAttrType {
    TableId(TableId),
    ColumnRef(usize),
    Const(i64),
    None,
}

pub struct RelNode {
    pub typ: RelNodeType,
    pub children: Vec<Arc<RelNode>>,
    pub data: Arc<RelAttrType>,
}

To construct a plan node,

pub fn join(
    left: impl Into<Arc<RelNode>>,
    right: impl Into<Arc<RelNode>>,
    cond: impl Into<Arc<RelNode>>,
) -> RelNode {
    RelNode {
        typ: RelNodeType::Join,
        children: vec![left.into(), right.into(), cond.into()],
        data: Arc::new(RelAttrType::None),
    }
}

pub fn scan(table: TableId) -> RelNode {
    RelNode {
        typ: RelNodeType::Scan,
        children: vec![],
        data: Arc::new(RelAttrType::TableId(table)),
    }
}

Note that we split the original plan node into 3 parts: the type of the plan node, the children of the plan node, and the data of the plan node. From a framework’s view, users will define RelNodeType and RelAttrType, and the RelNode should be defined inside the framework. If we go a step further, we can do something more generic like:

pub struct RelNode<T: RelNodeType, D: RelAttrType> {
    pub typ: T,
    pub children: Vec<Arc<RelNode<T, D>>>,
    pub data: Arc<D>,
}

The optimizer framework does not need to know what T: RelNodeType is and how many variants of plan nodes are there. The optimizer only compares, hashes, and clones the T. T can be an enum or a Box<dyn SomeTrait>, all up to the user. This representation also allows the optimizer to access and manipulate the children field directly. When the optimizer wants to convert the plan node into a different representation, it can keep the T and D and rewrite the children into the expected form.

And we can define all the plan structures we used in this blog post,

pub struct MemoRelNode {
    pub typ: RelNodeType,
    pub children: Vec<GroupId>,
    pub data: RelAttrType,
}

pub enum BindRelNode {
    RelNode {
        typ: RelNodeType,
        children: Vec<Arc<BindRelNode>>,
        data: Arc<RelAttrType>,
    },
    Group(GroupId),
}

// We will talk about this in the future
pub enum RelNodeMatcher {
    Match {
        typ: RelNodeType,
        children: Vec<RelNodeMatcher>,
    },
    Any
}

We won’t talk about how to convert between them in detail now, but we can imagine that such conversion code will not need to do a match on all variants of RelNodeType. Thus, when users add a new plan node, they only need to define the RelNodeType and RelAttrType, and the optimizer framework will take care of the rest.

On the user side, they are required to implement helper functions to interpret the structure of RelNode.

pub struct Join(Arc<RelNode>);

impl Join {
    pub fn left(&self) -> Arc<RelNode> {
        self.0.children[0].clone()
    }

    pub fn right(&self) -> Arc<RelNode> {
        self.0.children[1].clone()
    }

    pub fn cond(&self) -> Arc<RelNode> {
        self.0.children[2].clone()
    }
}

We can make such interpretations generic among RelNode, BindRelNode, and MemoRelNode so that a single impl can interpret all of them. In the following posts of this series of Lessons Learned from Writing a Query Optimizer, we will explore more about this plan representation and the Cascades/Volcano query optimization framework.

Do you think the proposed plan representation is a better alternative than the Apache Calcite representation? Feel free to comment and share your thoughts on the corresponding GitHub Discussion for this blog post.